Chapter 3 Dirichlet Process
Given a base distribution \(G_0\) over a measurable set \(\Theta\), and a concentration parameter \(\alpha\), we can obtain a Dirichlet Process
\[G\sim DP(\alpha,G_0).\]
The Dirichlet Process is a stochastic process, i.e., a distribution over function spaces. In particular, it is a distribution over probability measures (for example, probability functions on \(\mathbb{R}^D\)). Though \(G_0\) might be continuous, each draw from \(G\) would be a discrete probability distribution. Moreover, its marginal distribution follows a Dirichlet distribution. That is, if \(B_1,B_2,\ldots, B_r\) forms a partition on \(\Theta\), then (Teh, 2011)
\[\left( G(B_1),G(B_2),\ldots, G(B_r)\right)\sim Dir\left(\alpha G_0(B_1),\alpha G_0(B_2),\ldots, \alpha G_0(B_r)\right)\] Furthermore, we can show the following properties:
For any measurable set \(B\subset \Theta\)
\[\text{(i)}\qquad E[G(B)] = G_0(B) \] and
\[\text{(ii)}\qquad Var[G(B)] = \frac{G_0(B)(1-G_0(B))}{\alpha} \]
Property (ii) means that given the base distribution \(G_0\), the parameter \(\alpha\) is inversely proportional to the variance. As an extension, in the context of a Dirichlet prior in a Bayesian model, a larger \(\alpha\) implies a stronger prior.
3.1 Dirichlet Process Mixture Model (DPMM)
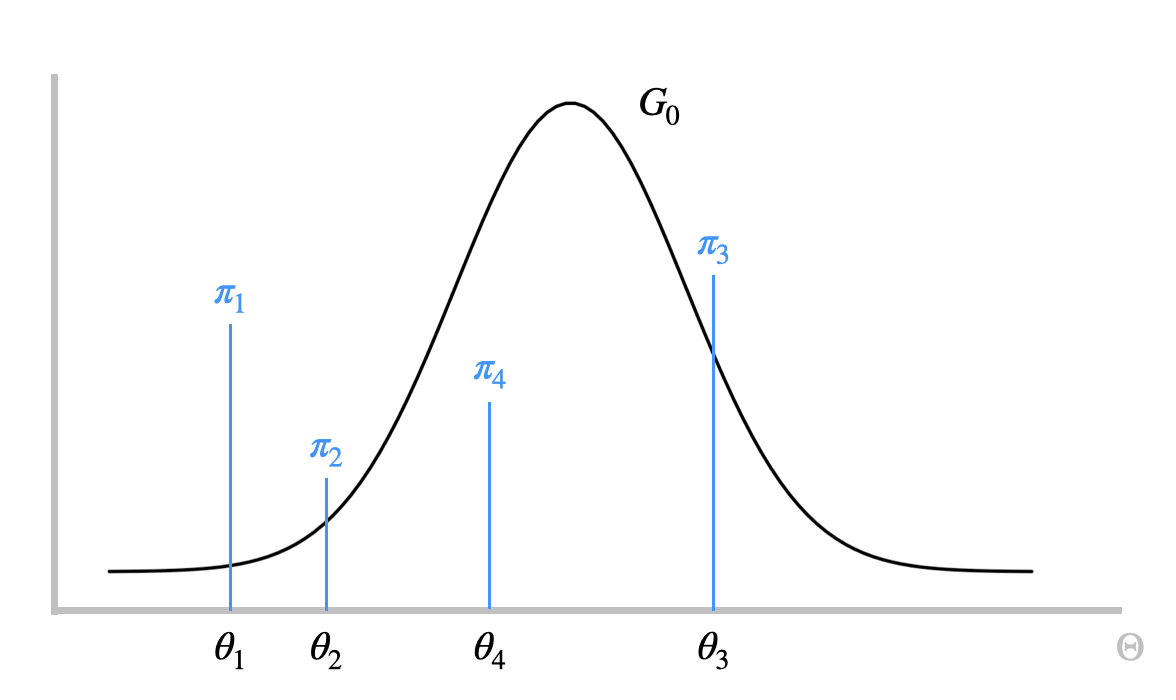
Figure 3.1: Dirichlet Process Mixture Model
We can use the Dirichlet process to build a mixture model that allows infinitely many components, i.e., the Dirichlet process mixture model (DPMM). Figure 3.1 is a visualization for a typical DPMM model.The observed data, \(x_1,x_2,\ldots,x_n\), is modeled by the set of latent parameters \(\theta_1,\theta_2,\ldots,\theta_n\) associated a kernel function \(F\), which are independently drawn from the distribution \(G\). Each \(x_k\) then follows the distribution \(F(\theta_k)\). Moreover, since \(G\) is a discrete distribution, it is possible for \(\theta_i=\theta_j\), in which case \(x_i\) and \(x_j\) come from the same component. As \(G\) is the mixing proportions, \(\pi_1,\pi_2,\ldots, \pi_n\) , are drawn from a GEM distribution with parameter \(\alpha\). Therefore, alternatively, we can describe the distribution of \(G\) as
\[G = \sum_{k=0}^\infty \pi_k\delta_k\]
Here, \(\delta_k\) is a point mass at \(\theta_k\). Alternatively, we can also view it as an indicator function about whether a data point \(x\) belongs to the \(k^{th}\) component.
Example
We will illustrate this idea by a Gaussian mixture model that assumes each component has the same standard deviation \(\sigma\) we already know. In this case, \(\theta_k\) is simply the center for each cluster, \(\mu_k\), for \(k=1,2,\ldots,n\), where each \(\mu_k\) is drawn from the base distribution \(G_0=Normal(\mu_0,\sigma_0)\).
\[x_k\mid \left(z_k,\left\{\theta^*_i\right\}\right) \sim Normal(\mu_{z_k},\sigma)\] \[z_k\mid\pi \overset{\text{i.i.d.}}{\sim} Mult(\pi)\]
\[\mu_k \overset{\text{i.i.d.}}{\sim} Normal(\mu_0,\sigma_0)\]
\[\pi\mid\alpha=\left(\pi_1,\pi_2,\ldots, \pi_n\right)\mid\alpha\sim GEM(\alpha) \] This can be summarized by the Dirichlet process model:
\[G = \sum_{k=1}^\infty \pi_k\delta_{\mu_k}\sim DP(\alpha,Normal(\mu_0,\sigma_0))\]
The following video illustrates the Dirichlet process mixture model as a generative model.
3.2 A Bayesian Perspective
The flexible nature of the Dirichlet process makes it one of the most widely-used Bayesian non-parametric models. Unlike a parametric prior that restricts the scope of inferences, a non-parametric prior has wide support. (Teh, 2011) Moreover, a natural extension of the Dirichlet-Multinomial conjugacy is the conjugacy for the Dirichlet process.
Given a set of observed values \(\theta_1,\theta_2,\ldots, \theta_n\) that takes values in \(\Theta\), and let \(B_1,B_2,\ldots,B_r\) be a finite partition of \(\Theta\), define \(n_k = \sum_{i=1}^n\delta_i(A_k)=|\{i:\theta_i\in B_k\}|\). We have
\[\left( G(B_1),G(B_2),\ldots, G(B_r)\right)\mid\theta_1,\theta_2,\ldots,\theta_n\sim Dir\left(\alpha G_0(B_1)+n_1,\alpha G_0(B_2)+n_2,\ldots, \alpha G_0(B_r)+n_r\right)\]
That is, the posterior distribution of \(G\) is also a Dirichlet process. Furthermore, we can show the posterior Dirichlet process has an updated concentration parameter of \(\alpha+n\) and updated base distribution \(\frac{\alpha G_0+\sum_{i=1}^n\delta_i}{a+n} = \frac{\alpha}{\alpha+n}G_0+\frac{n}{\alpha+n}\frac{\sum_{i=1}^n\delta_i}{n}\) (Teh, 2011):
\[G\mid \left(\theta_1,\theta_2,\ldots,\theta_n\right)\sim DP(\alpha+n,\frac{\alpha}{\alpha+n}G_0+\frac{n}{\alpha+n}\frac{\sum_{i=1}^n\delta_i}{n}) \] Thus, we can view the posterior base distribution as a weighted average between the prior base distribution \(G_0\) and the empirical distribution \(\frac{\sum_{i=1}^n\delta_i}{n}\). Moreover, on one hand, the smaller \(\alpha\) is, the smaller contribution \(G_0\) will have to the posterior base distribution; on the other hand, a large number of observations \(n\) would make the empirical distribution dominant the posterior.
3.3 Predictive Distribution
The posterior base distribution given observed \(\theta_k\) for \(k=1,2,\ldots,n\) is also the posterior predictive distribution for \(\theta_n+1\).
Let \(A\subset \Theta\). Since \(\theta_{n+1}\mid G,\theta_1,\theta_2,\ldots,\theta_k\sim G\), we have
\[\begin{align*} P(\theta_{n+1}\in A\mid \theta_1,\theta_2,\ldots,\theta_k)= &\int P(\theta_{n+1}\mid G,\theta_1,\theta_2,\ldots,\theta_k)P(G\mid \theta_1,\theta_2,\ldots,\theta_k)dP(G)\\ =&\int G(A)P(G\mid \theta_1,\theta_2,\ldots,\theta_k )dP(G)\\ =& E[(G(A)\mid \theta_1,\theta_2,\ldots,\theta_k]\\ =& \frac{1}{a+n}(aG_0(A)+\sum_{i=1}^n\delta_i(A)) \end{align*}\]
That is (Teh, 2011),
\[\theta_{n+1}\mid \theta_1,\theta_2,\ldots,\theta_k\sim \frac{1}{a+n}(aG_0+\sum_{i=1}^n\delta_i),\]
which can be described by the Blackwell-MacQueen urn scheme.
3.3.1 Blackwell-MacQueen Urn Scheme
The Blackwell-MacQueen urn scheme is a generalization of the Polya’s urn scheme described in Chapter 2 by allowing infinitely many colors. Specifically (Blackwell and MacQueen, 2013),
we assume the base distribution \(G_0\) is a distribution over colors, and each draw \(\theta_k\) represents a color. - We start with an empty urn.
On the \(k^{th}\) step
with probability \(\frac{a}{a+n}\), we pick a new color from the distribution \(G_0\) over the color space \(\Theta\), paint a new ball with this color, and put this ball to the urn;
with probability \(\frac{n}{a+n}\), we pick a random ball from the urn, record its color, paint a new ball with this existing color, and put the drawn ball and the new ball to the urn.
- in particular, in the second case, the probability to draw a ball with color \(\theta_k\) from the urn is proportional to \(n_k\), the existing number of balls in color \(\theta_k\).
The last observation above reflects a “rich-gets-richer” phenomenon. If we treat balls in the same color as a cluster, then larger clusters tend to grow faster. Suppose there are \(m\) clusters for the observed \(\theta_1,\theta_2,\ldots, \theta_n\). To reflect this view, we can also write the posterior predictive distribution as
\[\theta_{n+1}\mid \theta_1,\theta_2,\ldots,\theta_k\sim \frac{1}{a+n}(aG_0+\sum_{k=1}^m n_k\delta_k)\]
3.4 Appendix
3.4.1 Simulation Codes
The simulation for Section 3.1 is based on the codes (Broderick,n.d) below:
maxiters = 100
dpmm_sample <- function(
alpha = 2,
mu0 = 0,
sig_0 = 1.5,
sig = 0.3
) {
# Args:
# alpha: DP-stick-breaking/GEM parameter
# mu0: normal mean for cluster param prior (repeated twice)
# sig_0: normal sd for cluster param prior (covar is diag with this value)
# sig: nromal sd for points in a cluster (covar is diag with this value)
# some colors for the points in a cluster
palette(rainbow(10))
# set up the figure into two sized figures
par(mar = rep(2,4))
layout(matrix(c(1,2), 2, 1, byrow=TRUE),
heights=c(1,4)
)
# initializations
rho = c() # GEM-generated probabilities
rhosum = 0 # sum of probabilities generated so far
csum = c(0) # cumulative sums of probs gen'd so far
bar_colors = c() # colors to distinguish clusters
x = c() # points generated from the DPMM
z = c() # cluster assignments generated in the DPMM
mu = c() # cluster means generated in the DPMM
N = 0 # number of data points generated so far
newN = 0 # number of data points to generate next round (user input)
for(iter in 1:maxiters) {
print(iter)
# generate new DPMM data points
if(newN > 0) {
for(n in 1:newN) {
# uniform draw that decides which component is chosen
u = runif(1)
# instantiate components until the chosen
# one is reached
while(rhosum < u) {
# beta stick-break
V = rbeta(1,1,alpha)
# mass resulting from stick-break
newrho = (1-rhosum)*V
# update list of instantiated probabilities
rho = rbind(rho,newrho)
rhosum = rhosum + newrho
csum = c(csum, rhosum)
# fill in bars on the plot for
# instantiated probabilities
bar_colors = c(bar_colors,"grey")
# generate new cluster means for
# instantiated probabilities
newmu = rnorm(2,mu0,sig_0)
mu = rbind(mu, newmu)
}
# decide which cluster was chosen for this data point
thisz = max(which(csum < u))
z = c(z,thisz)
# generate a data point in this cluster
thismu = mu[thisz,]
newx = rnorm(cbind(1,1),thismu,cbind(sig,sig))
x = rbind(x,newx)
}
}
# record correct number of data points
N = N + newN
# plot the component probabilities instantiated so far
barplot(rbind(rho,1-rhosum),
beside=FALSE,
horiz=TRUE,
col=c(bar_colors, "white"), # remaining mass in (0,1)
ylim=c(0,1),
width=0.7,
main=bquote(rho~"~GEM("~.(alpha)~")")
)
# after initial display, plot how the next
# component is chosen
if(N > 0) {
points(u, 1, pch=25, col="red", bg="red")
}
# just gets the labels and figure limits right
# real plot still to come
plot(x,
pch=".",
xlim=c(-5,5),
ylim=c(-5,5),
main=paste("N = ", toString(N),
", #means = ", toString(length(rho)),
", #clust = ", toString(length(unique(z))),sep="")
)
# plot all the instantiated means
points(mu,
pch=15,
col="black"
)
# plot the data points generated from the DPMM thus far
points(x,
pch=19,
col=z
)
# Generate one new draw for each press of "enter".
# Writing a number generates that many new samples.
# Press 'x' when finished
line <- readline()
if(line == "x") {
return("done")
} else if(line == "") {
newN = 1
} else {
newN = as.numeric(line)
}
}
}
dpmm_sample()Reference
Blackwell, D., and MacQueen, J. B. (1973) Ferguson Distributions via Polya urnSchemes, The Annals of Statistics, 1, 353-355
Broderick, T. (n.d.). Tutorial of Bayesian Nonparametric. Tamara Broderick. Retrieved November 13, 2021, from https://tamarabroderick.com/tutorials.html.
Khalid, El-Arini. (2008) Dirichlet Processes A gentle tutorial, Select Lab Meeting
Teh Y. (2011) Dirichlet Process. In: Sammut C., Webb G.I. (eds) Encyclopedia of Machine Learning. Springer, Boston, MA. https://doi.org/10.1007/978-0-387-30164-8_219